シミュレーターのための自動車物理
タイヤのトラクション,ブレーキ,転がり抵抗,空気抵抗,遠心力を使用したシミュレーターを考える.簡単のために自動車は平面上を移動するものとし,段差を考慮しない.
概要
車体にかかる力をすべて計算して,数値計算により速度ベクトルと位置ベクトルとを計算する.
車体にかかる以下の力を計算により求める.太字表記はベクトルを表す.
これらを足し合わせれば車体にかかっている力が求まる.上下の移動を考慮しないので,重力は計算に入っていない.Faero と Frr と Fbrake とは Ftractionと逆向きであることに注意.
F = Ftraction + Faero + Frr + Fc + Fbrake + Fcf
力がわかれば,加速度ベクトルは運動の第2法則で計算できる.
a = F/m
a:車の加速度 [m/s2]
m:車の質量 [kg]
車の速度ベクトル v[m/s] は加速度ベクトルを時間に関して積分することで求められる.シミュレーターで積分を計算するには,オイラー法やホイン(Heun)法,ルンゲ=クッタ法を使う.オイラー法を使う場合は以下のようになる.
v = v + dt・a
dt:前フレームからの経過時間[s]
車の位置 pも同様に計算できる.
p = p + dt・v
加速度の省略
加速度から一度に位置を計算するには以下のようになる.
p = p + v・dt + 0.5・a・dt2
フレームレートが高い場合は加速度の項は非常に小さな値になるため,加速度の項を省くことがある.
空気抵抗
車の空気抵抗は圧力抵抗と摩擦抵抗との和で表現できる.圧力抵抗は車体前後の圧力差によって生じる抵抗で,以下の4つに分類できる.
- 形状抵抗:車の形によってきまる抵抗.圧力抵抗のほとんどがこれである
- 凹凸抵抗:ミラーやウイング等の突起物による抵抗
- 吹き抜け空気抵抗:エンジンの冷却や車内の換気によっておこる抵抗.ラジエータから機関室への空気の吹き抜けの影響が大きい
- 誘導抵抗:車体を上方へ持ち上げる揚力によって引き起こされる抵抗
摩擦抵抗は車体表面とそれに触れている空気との間の摩擦によって生じる抵抗だ.
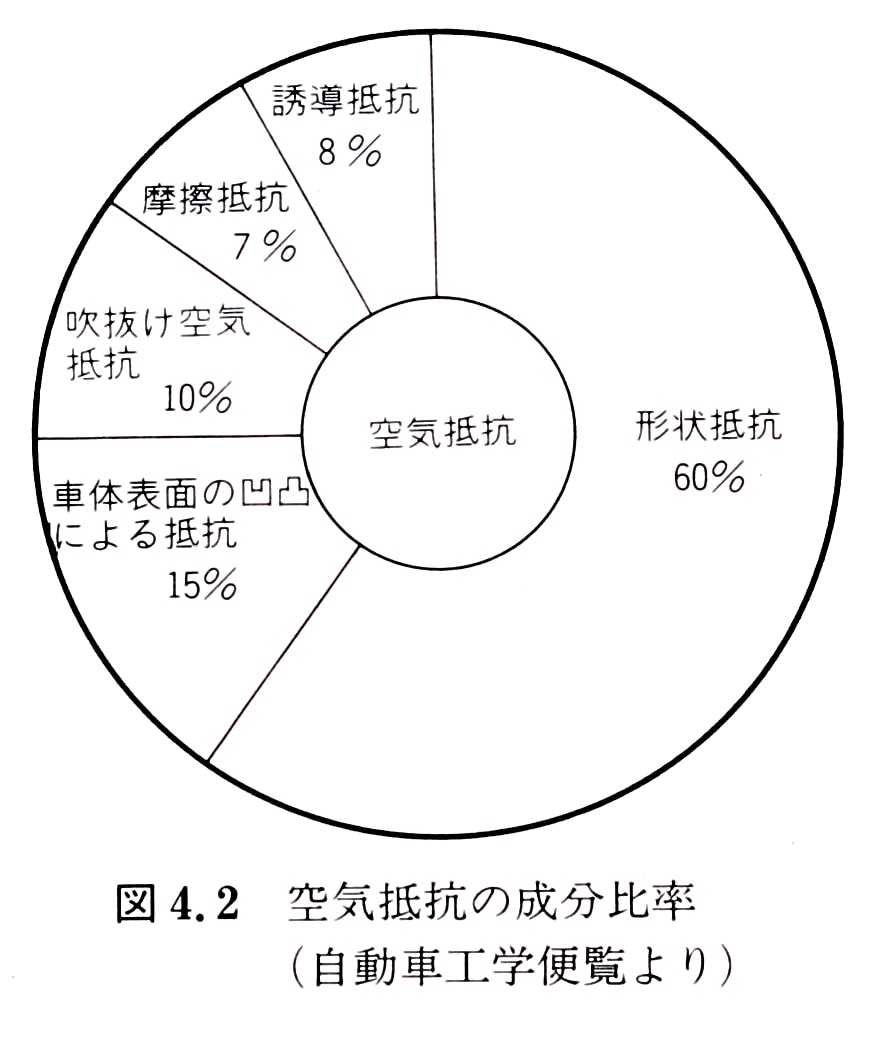
空気抵抗におけるそれぞれの要素の影響力の割合は一般車両では以下のようになる.
これらの要素を単純化すると空気抵抗 Faero[N] は以下の式になる.
ρ:空気の密度 [kg/m3]
Cd:空気抵抗係数
A :自動車の正面投影面積 [m2]
v:進行方向における自動車の空気に対する相対速度 [m/s]
空気の密度は以下の式で計算できる.ちなみに 0℃,1 atm の状況での空気の密度 ρ は 1.293 kg/m3である.
t:気温 [℃]
P:大気圧 [atm]
e:水蒸気圧 [atm]
以下の表は空気抵抗係数 Cdの概略値である.
自動車の種類
| Cd
|
乗用車
| 0.3~0.5
|
トラック
| 0.4~0.6
|
バス
| 0.5~0.8
|
二輪車
| 0.6~0.9
|
自動車の正面投影面積 A が明確でない場合は以下の近似式のどちらかを使う.
- トレッド幅・全高
- 全高・全幅・0.8
転がり抵抗
転がり抵抗は,タイヤの変形,路面の凸凹,タイヤが路面上を部分的に滑るためにおこる摩擦などによって引き起こされる.これを計算するのは困難なので,転がり抵抗はタイヤにかかる荷重に比例すると考え以下の式で表す.
Frr= u・μrW
Frr:転がり抵抗 [N]
u:トラクションと逆向きの,転がり抵抗の働く方向を示す単位ベクトル
μr:転がり抵抗係数
W:タイヤに加わる荷重 [N]
| 道路条件 | μr |
| 乾いた砂地 | 約0.25 |
| 砂または石灰質の道 | 約0.17 |
| 新しく砂利を敷いた道 | 約0.13 |
| 石の多い凸凹道 | 約0.08 |
| 手入れのよい小砂利道 | 約0.03 |
| アスファルトまたはコンクリート道 | 約0.015 |
トラクションがかかっていなくてもタイヤが地面上を転がるなら転がり抵抗は発生する.
転がり抵抗はこのほか車速,タイヤの空気圧,タイヤ構造などによって変わる.車速に比例して転がり抵抗はわずかに上昇する.車速が 140 km/h 以上になるとスタンディングウェーブの発生により転がり抵抗が急増する.タイヤの空気圧増加率の半分くらいの割合で転がり抵抗は減少する.
低速では転がり抵抗が主な抵抗力である.高速では空気抵抗がそれにとって代わる.100 km/h ぐらいで両者が一致する[Car Physics].
タイヤにかかる荷重
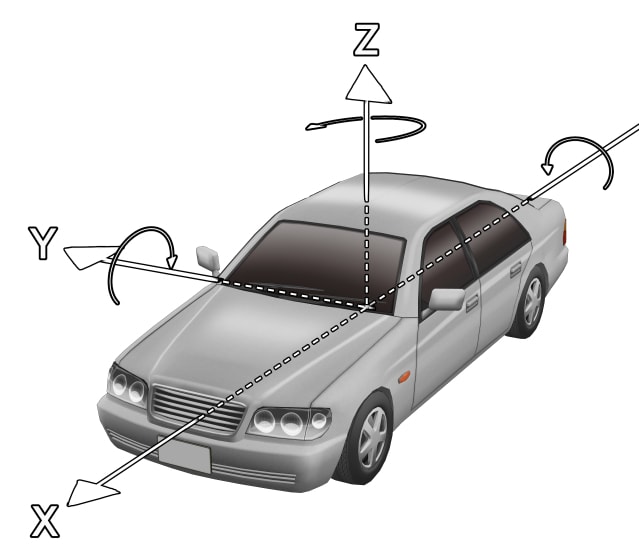
トラクション,ブレーキ,転がり抵抗等を計算するにはタイヤにかかる荷重を計算する必要がある.タイヤにかかる荷重は X 軸回り(ロール)の回転による荷重と,Y 軸周り(ピッチ)の荷重とをかけ合わせれば計算できる.
タイヤにかかる荷重は タイヤにかかる荷重の計算を参照.
ピッチ方向の傾きを φ [rad],ロール方向の傾きを Θ [rad] とすると,フロントとリアの荷重配分比率は以下のようになる.実際のタイヤの荷重はそれぞれふたつの荷重式と車の重量[N]とを掛け合わせばいい.4輪の荷重をすべて合計すると車の重量と一致する.
W:車の重量 [N]
L:ホイールベース [m]
h:地面から重心までの高さ [m]
t:トレッド幅 [m]
φ:Y 軸(ピッチ)周りの車体の傾き [rad]
Θ:X 軸(ロール)周りの車体の傾き [rad]
c:重心から後輪までの長さ [m]
a:進行方向への加速度 [m/s2]
g:重力加速度 [m/s2]
V:速度[m/s]
R:旋回半径[m]
進行方向への加速度は減速時には符号を反転させる.旋回半径は遠心力の項目を参照.
タイヤの接地判定
タイヤが接地していないとき,その荷重を0で計算する.
トラクション
エンジンがタイヤを回転させるトルク [N・m] はエンジンの回転数,エンジンの出力,現在のギア,タイヤの半径,スロットル等に影響される.エンジンが車に与える速度変化 [N] は以下の式で表現できる.
Ftraction = u・Tengine・rt・xg・xd・n / Rtire
u:前輪向きを表現している単位ベクトル
Tengine:現在の回転数のときのエンジンのトルク [N・m]
rt:スロットル
xg:ギア比
xd:デフ比
n:トランスミッション効率
Rtire:タイヤの半径 [m]
トランスミッション効率は MT 95%以上,CVT 低速=85% 高速=75%,AT 低速=80% 高速=90% と言われている.
Ftractionの大きさがタイヤの μsW を超えるとタイヤはスリップする.この μs はタイヤと路面との摩擦係数で転がり抵抗係数とは別のものである.μs についてはタイヤのスキッド限界を参照.
ギア比やデフ比を大きくすればいくらでもトルクは大きくなる.しかしそうするとタイヤの角速度――つまり最高速度――が低下する.ギア比やデフ比を大きくするとすぐにエンジンの回転数の上限に達し,加速できなくなる.
エンジンのトルクは 1000 rpm もしくは 500 rpm 区切り(望むならもっと細かくてもいい)の配列で表現する.現在の回転数に応じてそれを線形補間してトルクを計算する.
エンジンの RPM の計算
タイヤが接地しているならば,エンジンの回転数 [rpm] は車速やタイヤ半径などの影響を受ける.現在の車速 v [m/s] ,タイヤの半径 r [m],ギア比 xg,デフ比 xdとすると,エンジンの回転数 [rpm] は以下の式で計算できる.
rpm = v/(2・π・r)・60・xg・xd
大抵のエンジンは 1000 rpm 以下の回転数の時のトルクを定義していない.シミュレーターがエンストを許さないなら,そのような状態になったときはクラッチを切りアイドリング状態に移行する処理を追加する.
スリップ比とトラクションとの関係
スリップ比は摩擦係数だけでなくトラクションによっても変化する.現在のタイヤのトルクからスリップ比を取得し,RPM を修正する.
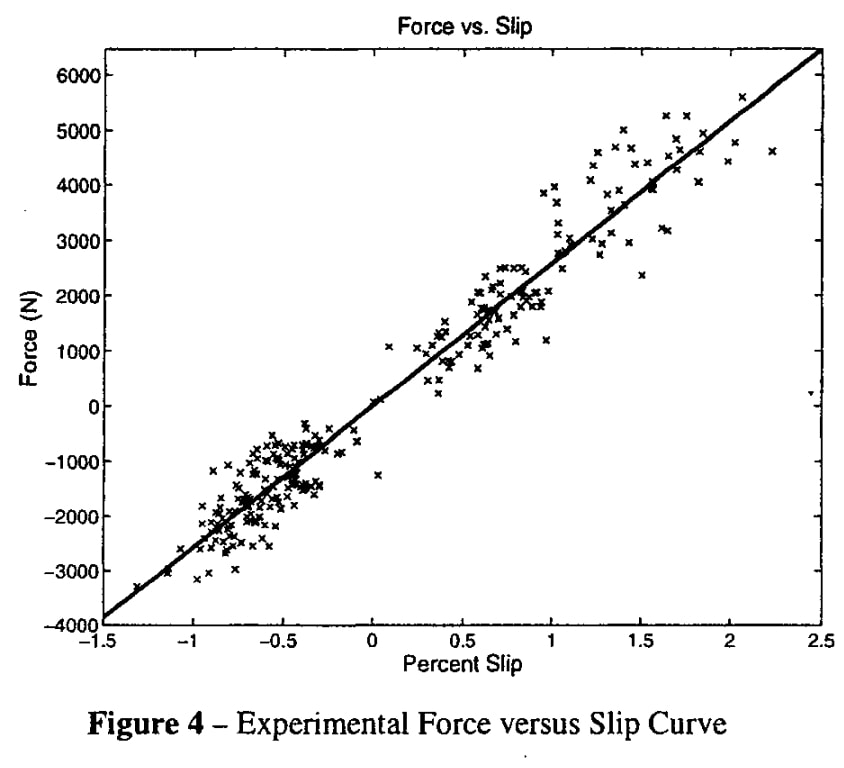
『Calculating Longitudinal Wheel Slip and Tire Parameters Using GPS Velocity』Shannon L. Miller ほか著 1804項 図4 より転載
このグラフを数式にすると,スリップ比 = Ftraction/2000 になる.トラクションが 4000[N] のとき,スリップ比は 2%.よって RPM・1.02 が実際の RPM になる.
遠心力
ハンドルを切ると車体には遠心力 Fc[N] がかかる.これは速度の2乗に比例して大きくなる.速度が速いほどコーナーが曲がりにくくなる原因の一つが遠心力である.
旋回半径を R [m],角速度を ω [rad/s] とすると遠心力は ω2R [m/s2].ωR = V なのでこれは V2/R と書き換えられる.重心に働く遠心力 [N] は以下の式で計算できる.
W:車の重量[N]
g:重力加速度[m/s2]
V:車の速度[m/s]
R:旋回半径[m]
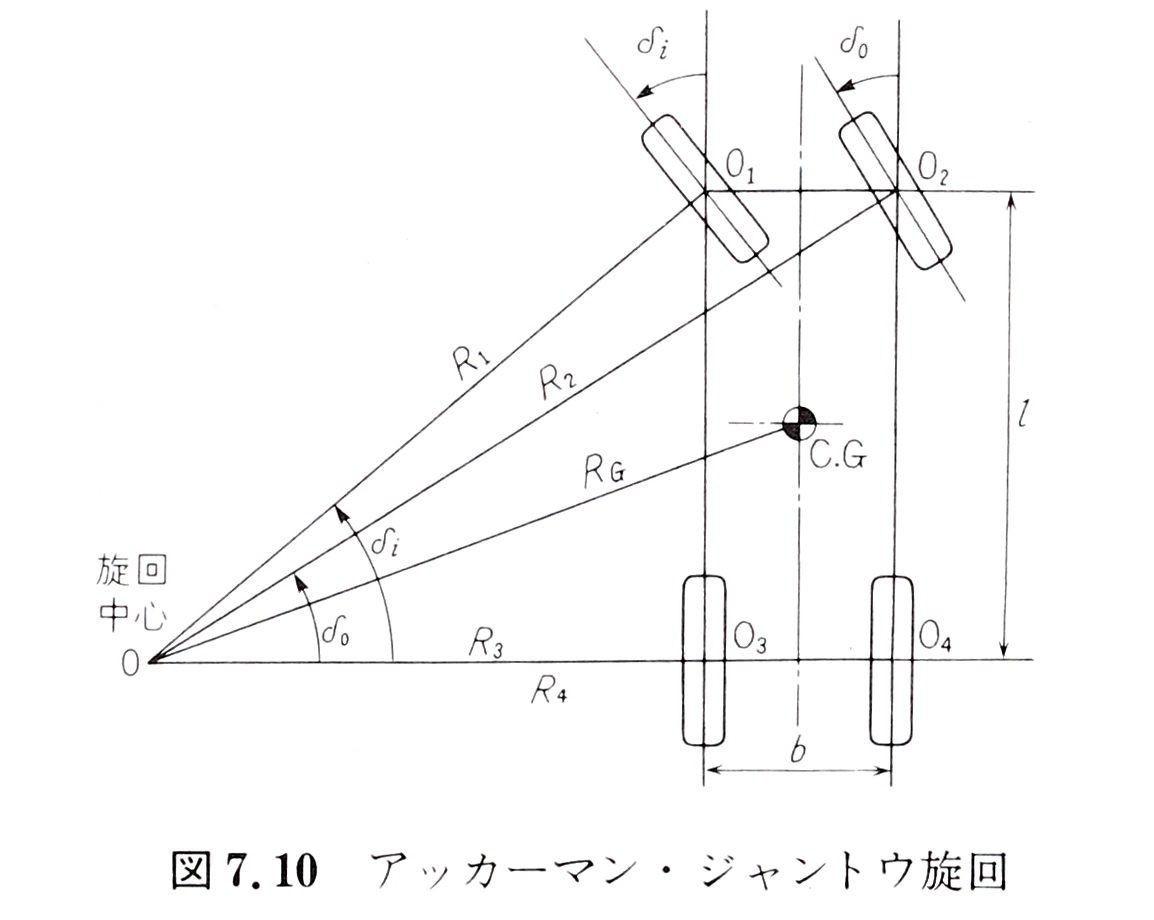
旋回半径はアッカーマンアングルを利用して求める.これは遠心力が発生しないぐらい低速で旋回するときのモデルであるため,定常旋回時の旋回半径とは異なる.
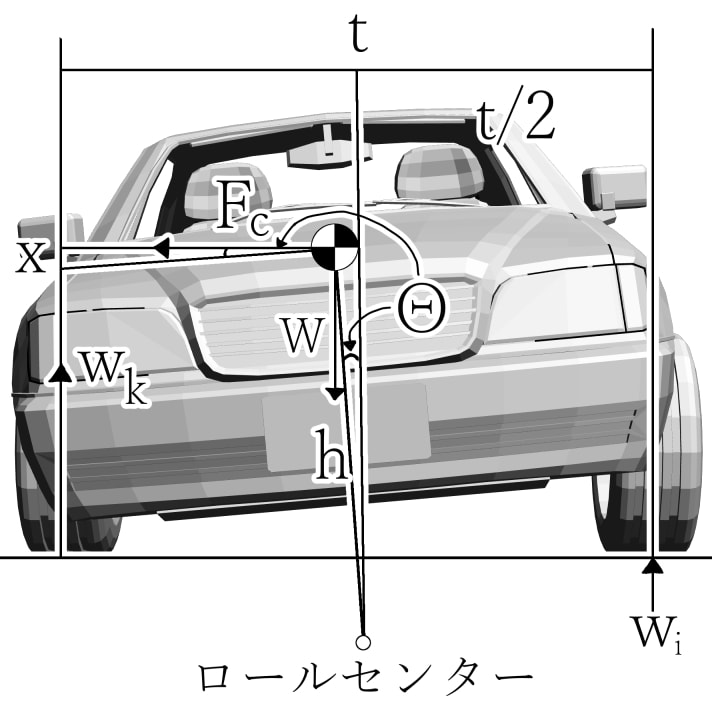
R1を旋回半径 R [m] として使う場合,旋回半径は以下の式で計算できる.
l:ホイールベース[m]
δi:前輪の実舵角[rad]
車体のロール/ピッチ角度の計算
遠心力を受けたり,加減速したりすると車体にモメントが発生し,回転運動を生じる.そのときの車体の傾きは,車高を下げたり,サスペンションのばね乗数を大きくしたりして調整できる.
サスペンションは追加のモメント ΔW [N・m]を受け,その分だけ沈む.ΔW は Fc・h + W・h・tanΘ だ.サスペンションの反発力 wk [N]は k・x で表現できる;x はサスペンションが沈み込んだ距離[m]で,k はばね乗数[N/m]だ.サスペンションが沈み込んだ距離 x は (t/2)・tanΘで,Θ << 1 のとき tanΘ ≒ Θ[rad] で近似できて,x=tΘ/2 になる.
最終的なサスペンションの反発モメント[N・m] は t2kΘ/2 になる.Fc・h は遠心力によるモメントで,W・h・tanΘ は車体の傾きで生じる重力によるモメントだ.結局,車体のロール角度[rad] は以下の式になる.
Fc:遠心力[N]
h:ロールセンターから重心までの距離[m]
t:トレッド幅[m]
k:ばね乗数[N/m]
ただしばね乗数 k は前後輪のばね乗数の合計で,前輪のばね乗数を kf,後輪のばね乗数を kr とすると,k = kf + kr である.
この t2k/2 の項は一般的にロール剛性[N/rad] と呼ばれる.
シャシー形式ごとのロールセンターの求め方はロールセンターの求め方を参照.
加減速時のピッチ角度も同様に計算できて,以下の式になる.
φaccel:加速時のピッチ角度
φbrake:減速時のピッチ角度
Fa:加減速力[N]
lr:重心から後輪までの長さ[m]
ll:重心から前輪までの長さ[m]
L:ホイールベース[m]
コーナリングフォース
横滑り角
横滑り角は実舵角と車の進行方向との間の角度である.現在フレームの車の進行方向を計算するのに横滑り角が必要なので,ひとつ前のフレームの車の進行方向と現在フレームの実舵角とから横滑り角を計算する.
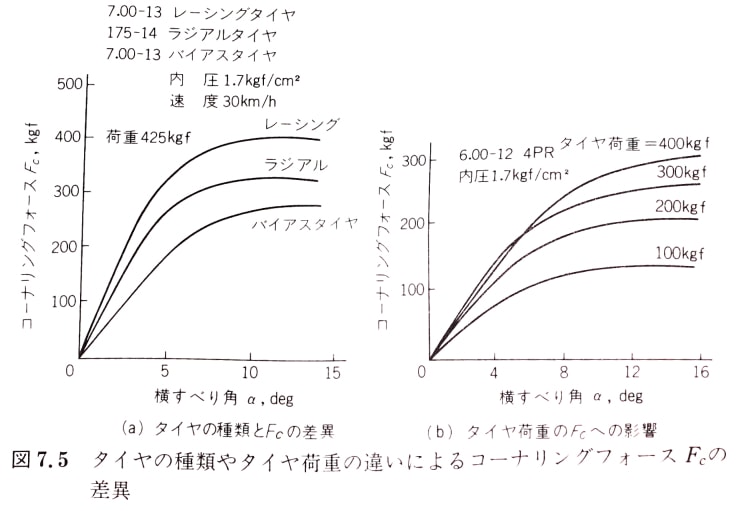
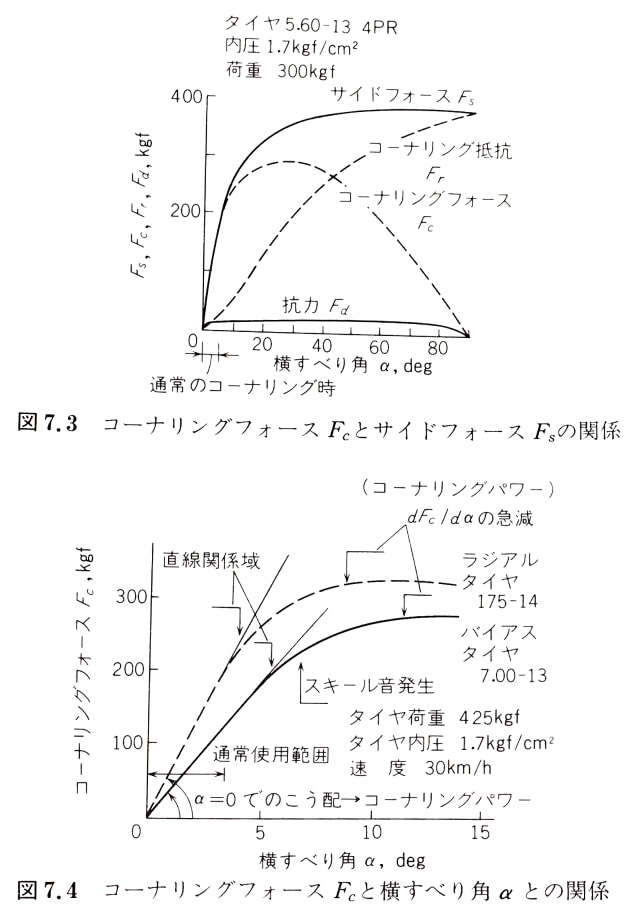
ステアリングを切り,横滑り角が発生すると遠心力の働く方向にタイヤがねじれる.このときのタイヤが元の形に戻ろうとする力がコーナリングパワーだ.コーナリングパワー [N/rad] はタイヤに固有のコーナリング特性で, 単位横滑り角あたりのコーナリングフォース[N]を示している.コーナリングパワーはタイヤ荷重やタイヤ内圧,横滑り角の増加とともに増加する.ただし横滑り角がある閾値を超えると,コーナリングフォースは減少し頭打ちが発生する.引用した図(自動車の運動と制御)では,横滑り角が約4°までは直線的にコーナリングフォースが増加する.しかしそこから次第にコーナリングフォースは減少し,横滑り角が約10°でコーナリングフォースは飽和している.コーナリングフォースはそのほかにもタイヤのプライ数,コードクラウン角度,ブレーカ,トレッドパターン,アスペクト比に影響を受ける.
コーナリングフォース Fc[N] はコーナリングパワー[N/rad]と横滑り角とから計算できるが,それを単純な関数で表現するのは難しい.いくつかの直線で近似するか,テーブルにデータを保存しておき参照するかして取得する.
横滑り角からコーナリングパワーを計算する関数を fcp(α) とするとコーナリングフォースは以下の式で計算できる.
Fcf = T・fcp(α)
T:コーナリングパワーの働く方向.車体の進行方向に直角
f:コーナリングパワーを計算する関数[N]
α:横滑り角
コーナリングパワーの働く方向 T は車体の進行方向と世界の上向きベクトル(たいていは(0, 1, 0))との外積をとることで計算できる.車体の進行方向は,前フレームに計算した速度ベクトルを正規化したものを使う.
ブレーキ
タイヤのスキッド限界
トラクションやコーナリングフォースがタイヤのスキッド限界を超えるとスリップする.コーナー中にトラクションを掛けたり,ブレーキしたりするとその力と遠心力とでタイヤの制駆動力を使用してしまい,コーナーを曲がるのに使うコーナリングフォースが減少する.タイヤのスキッド限界はタイヤにかかる荷重,タイヤの温度,タイヤの損耗具合,タイヤの摩擦係数に依存する.近似としては Fskid[N] は μsW で近似する.W はタイヤにかかる荷重.μs は摩擦係数で,乾いたアスファルトでは 0.7~0.8,濡れていると 0.4~0.5,雪道では 0.1~0.2 ぐらいになる.
ブレーキの発生させる制動力
ブレーキの発生させる制動力とタイヤのスキッド限界とは別物である.たとえばタイヤのスキッド限界が 4000[N] だとしよう.この車に 6000[N] の制動力をかけても無意味だ;そうしても単にタイヤがロックされてスリップするだけだからだ.もちろんスキッド限界をわずかに超える制動力を設定するのは問題ない.
制動力はタイヤの半径とタイヤの摩擦係数とタイヤの空気圧とに依存する.タイヤの半径を大きくすれば最高速が伸びる.しかしブレーキ時の地面がタイヤを引っ張る力も大きくなり,それだけ強力なブレーキが必要になる.空気圧が高ければ接地面積が狭くなり制動力はおちる,逆に空気圧が低ければ制動力は増す.
制動力 Fb[N] は以下の式で表現できる.
Fb = u・rbrake・Bmax
u:トラクションと逆向きの,制動力が働く方向を示す単位ベクトル
rbrake:ブレーキの踏み込み具合
Bmax[N]:最大制動力
コーナー中にトラクションを発生させたり,制動力をかけたりするとその分だけコーナリングフォースが減少する.
前輪と後輪とのブレーキの強さは普通同じにしない.減速時には前輪により多く荷重がかかるため前輪はブレーキの効きが強く,後輪はブレーキの効きが弱くなる.そのため普通は前輪のブレーキ力を強く,後輪のブレーキ力を弱く設定する.
車速が 0 付近のとき,ブレーキに特別な処理が必要になる.そうしないと車が勝手に後退してしまう.
ある減加速度 a [m/s2] が必要な時の各タイヤのブレーキ力 Bx[N] は Wxをそれぞれのタイヤの荷重とすると,以下の式で計算できる.
Bx = Wx・a/g
路面の温度が低いとタイヤが温まりにくく,グリップが悪くなる.
まとめ
車オブジェクトが持っている定数
質量 [kg]
ホイールベース [m]
地面から重心までの高さ [m]
トレッド幅 [m]
重心から後輪までの長さ [m]
タイヤの半径 [m]
ギア比テーブル
デフ比
エンジンのトルクテーブル [N・m]
タイヤの最大舵角 [rad]
タイヤのスキッド限界
最大制動力[N]
車オブジェクトが持っている状態変数
位置ベクトル[m]
速度ベクトル[m/s]
エンジンの回転数 [rpm]
ハンドルの回転度合 [rad]
ゲームでは1フレームの間にステアを非現実的な速度で操作できるため, それを補正するために現在のハンドルの回転度合を保存しておく.
外部から渡されるパラメータ/環境が持っている変数
空気の密度 [kg/m3]
空気抵抗係数
風の向きベクトル [m/s]
気温 [℃]
大気圧 [atm]
水蒸気圧 [atm]
路面の転がり抵抗係数
路面とタイヤとの摩擦係数
路面の法線ベクトル
ユーザーからの入力
アクセルの踏み込み具合
ブレーキの踏み込み具合
ステアリングアングル
計算過程
- エンジンの踏み込み量とハンドルの回転角度を取得
- トラクションを計算
- 空気抵抗を計算
- 転がり抵抗を計算
- 遠心力を計算
- コーナリングパワーを計算
- 制動力を計算
- 車にかかる力を計算
- 加速度を計算
- 速度を計算
- 位置を計算
- 速度からエンジンの回転数を再計算
参考文献
[自動車工学編集委員会]自動車工学
[安部正人]自動車の運動と制御
VehicleDynamicsForRacingGames(pdf)
Calculating Longitudinal Wheel Slip and Tire Parameters Using GPS Velocity(pdf)
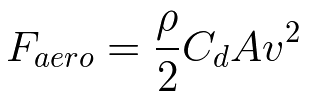
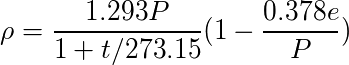
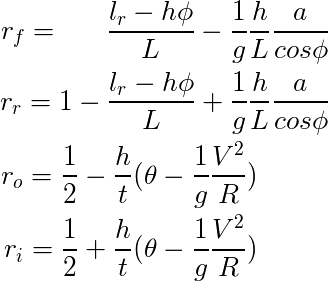
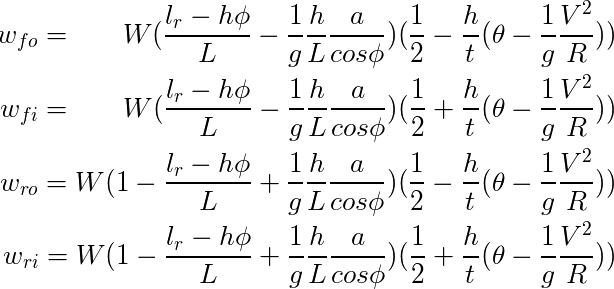
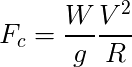
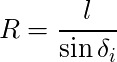
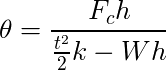
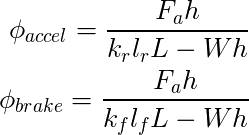
![『自動車の運動と制御[第2版]』安部正人著 東京電機大学出版局発行 21頁 図2.16 より転載](../images/car-physics-cf3.jpg)