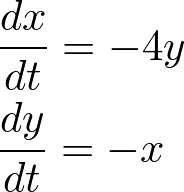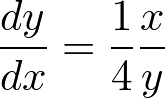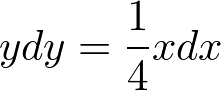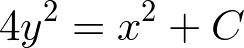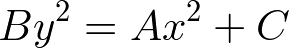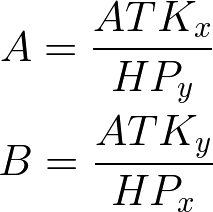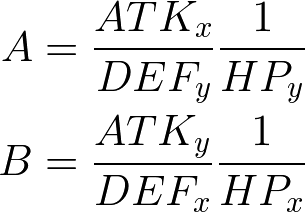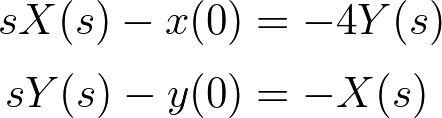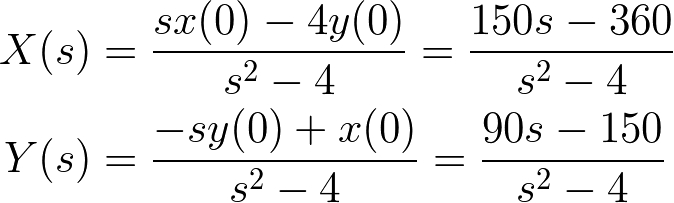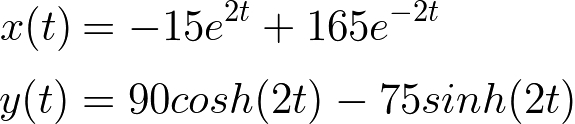簡単なランチェスターの法則

カテゴリ：others

ランチェスターの法則を使うとストラテジーゲームで、戦闘を始める前に勝敗と残存人数とを概算できる。

ランチェスターの法則はいくつか前提条件がある。大雑把に言うと、チームメンバーの装備・体力などのステータスが全員同じで、敵全体に攻撃可能という前提だ。

例

戦闘力係数（fighting effectiveness coefficients）１・初期人数 150 のチーム X と、戦闘力係数４・初期人数 90 のチーム Y とが戦闘したとする。そのときどちらが勝ち、戦闘終了時の残存人数はいくらだろうか。これを式にすると以下のようになる。

式１

式を整理

変数分離形にした後、積分する。

変数分離形

積分後

積分定数 C は X と Y とに初期人数を代入することで計算できる。この例では 9900 になる。積分定数が正のとき Y が勝ち、負の時は X が勝つ。

戦闘終了時の残存人数は X（Xが勝つときはY）に 0 を代入して解く。この例では Y に約 49 人残る。

この式を一般化すると以下のようになる。By² > Ax² のとき Y が勝ち、By² < Ax² のとき X が勝つ。

一般化された式
A：X の戦闘力係数
B：Y の戦闘力係数
C：積分定数

HP と攻撃力とで戦闘力係数を調整する。たとえば X の HP と攻撃力とをそれぞれ HP_x・ATK_x、Y は HP_y・ATK_yとすると、戦闘力係数を次のようにすればいい。

式6

攻撃力ー防御力を計算して０以下ならダメージ０とするか、攻撃力/防御力とする。

防御力を追加

敵の HP*DEF を固さ（solidity）と定義すると、戦闘力係数は ATK/SOL になる。

ラプラス変換を使って方程式を解けば、戦闘にかかる時間も計算できる。

方程式（再掲）

ラプラス変換後の方程式
X(s)：x(t) のラプラス変換
Y(s)：y(t) のラプラス変換

X(s),Y(s) について解く

解を逆ラプラス変換すると以下の式になる。

最終的な解

x(t) = 0 とすると t を計算できる。

t = log(11)/4 = 0.559 になる。