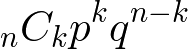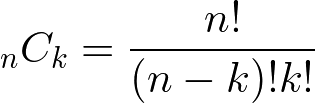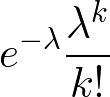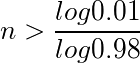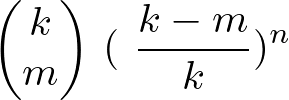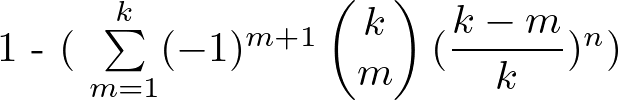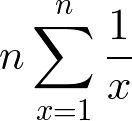ガチャの確率計算
計算器はこちら。
目次
当選確率 1% のガチャを 100 回やったときに、ひとつ以上あたる確率は?
当選確率 2% のガチャを 100 回やったときに、ふたつ以上あたる確率は?
当選確率 1%、天井 100 回のガチャがある。このガチャを 250 回やって、5枚あたりが手に入る確率は?
当選確率 2% のガチャを 99% の確率で手に入れるには何回やればいいか?
当選確率 1% のガチャを 100 回やったときに、ひとつ以上あたる確率は?
これは外れる確率 99% のガチャを 100 回連続で外す現象の余事象だ。つまり
1 - 0.99100 = 63.4%
Google でべき乗を計算するのには ^ を使う。以下の式で Google 検索すると、上記の式を計算できる。
1 - 0.99^100
当選確率 2% のガチャを 100 回やったときに、ふたつ以上あたる確率は?
これは1回も当たらない確率と1回だけ当たる確率とを足し合わせたものの余事象だ。特定回数だけ当たる確率は2項分布で計算できる。
n:試行回数
k:あたりの当たる回数
p:当選確率
q:外れる確率 = 1-p
一度も当たらない確率は 0.98100 で、一度だけ当たる確率は 100C10.0210.9899 だ。計算式は以下のようになる。
1 -0.98100 -100C10.0210.9899 = 1 -0.98100 -2*(0.9899) = 0.597 ≒ 60%
組み合わせ(nCk)はWolframAlphaで計算できる。計算するには検索窓に C(n,k) を入力する。上記の例では C(100,1) になる。結果は Result の場所に表示される。
ポアソン分布
ガチャのような発生確率が稀で試行回数の多い事象の場合、特定回数だけあたる確率はポアソン分布で近似できる。
λ:平均(当選確率 * 試行回数)
k:計算したい当選回数
上記の例の問題をポアソン分布で計算すると、一度も当たらない確率は 0.135 で、一度だけ当たる確率は 0.271。1 - 0.135 - 0.271 = 0.594 ≒ 59%。
当選確率 1%、天井 100 回のガチャがある。このガチャを 250 回やって、5枚あたりが手に入る確率は?
200 回やっているので2枚は確実に手に入る。よって 250 回で3枚以上手に入る確率を計算する。計算方法は当選確率 2% のガチャを 100 回やったときに、ふたつ以上あたる確率は?を参照。
結果は 45.68%。300 回だと 80.24%。
10 連の最低保証込みの取得確率は?
当選確率 1%。ただし 10 回に1回は最低保証モードに切り替わり当選確率2%になるガチャがある。このガチャを 100 回やったときに当たりが1枚以上手に入る確率を考える。
最低保証の発生回数は 10/100 = 10 回、通常ガチャの発生回数は 100 - 10 = 90回。あとは単に1から 10 回 * 2% の結果と 90 回 * 1% との掛け算の結果を引けばいい。計算式は以下のようになり、結果は約 66.9 %。
1 - (0.9810) * (0.9990) = 0.6693045110
当選確率 2% のガチャを 99% の確率で手に入れるには何回やればいいか?
これは 98% の確率で外れるガチャが連続で外れる確率を 1% 以下にするには何回やればいいか?という問題と同じだ。式は以下のようになる。
0.98n < 0.01
両辺の対数をとると n * log 0.98 < log 0.01 よって
log 0.98 < 0 なので不等号は反転している。
最終的に n ≒ 228 になる。
log の計算は Google でもできる。Google 検索で log0.01/log0.98 と入力すると計算できる。
コンプガチャの確率計算
1 から「コンプできない確率」を引くことで計算する。
コンプできない確率は特定種類しかそろわない確率を合計することで計算するが、計算に重複が発生するので包除原理を使って、適宜引き算を挿入する。
確率計算
特定種類しか手に入れられない確率の計算
3種類しかないコンプガチャを n 回引くとする。このとき1種類しか手に入らない確率は 3 * (1/3)n。(1/3)n が特定種類だけを引き続ける確率で、係数の3が3種類分。係数は組み合わせで計算できて C(3,1) = 3。組み合わせはWolframAlphaで計算できる。
同様に、2種類しか手に入らない確率は (2/3)n で、係数は C(3, 2) = 3。よって 3 * (2/3)n
特定種類しか引けない確率を一般化すると以下の式になる。
包除原理
3種類をそれぞれ A, B, C と表記する。A だけがでない確率を計算したときに、A と B とがでない確率の計算と A と C とがでない確率の計算と A と B と C とがでない確率の計算も含まれる。そして B だけや C だけがでない確率を計算するときにこれらの確率が重複してしまう。このような計算を引き算する必要がある。詳細は Wikipedia の包除原理を参照。
計算式
コンプできる確率は以下のようになる。
外部リンク
Coupon collector's problem(日本語)
期待値計算
ガチャの期待値(期待回数)の計算
1%の確率であたりが当たる場合、その期待値 n は 1 = n * 0.01 で計算できる。この場合 n は 100 だ(ただし実際に 100 回やったときにあたりの出る"確率"は 63.4 %だ)。
2種類しかない場合
最初の1枚はダブらないので期待値は1。2枚目は 1/2 の確率でダブるので、あたりの当たる確率も 1/2。よってその期待値は2。合計 1 + 2 = 3 回がこのコンプガチャの期待値だ。
3種類ある場合
最初の1枚はダブらないので期待値は1。2枚目は 1/3 の確率でダブるので、ダブらない(あたりの当たる)確率は 2/3。よってその期待値は3/2。3枚目は 2/3 の確率でダブるので、ダブらない確率は 1/3。よってその期待値は3。合計は 1 + 3/2 + 3 = 5.5 回が3種類ある場合のコンプガチャの期待値だ。
一般化
n 種類あるコンプガチャをコンプするのに必要な回数の期待値は以下のようになる。
期待値ベースのコンプガチャの確率計算
期待回数 n がわかれば確率 p は p = 1/n で計算できるが、引く回数が少ない場合はこの方法は誤差が大きい。
2種類の場合
必ずダブらない1回目を無視するとコンプできる確率は 50 %。期待値から計算した確率は 66.6 %。
3種類の場合
3種類以上の場合の確率を計算するには引く回数を指定する必要がある。
4回引く場合
必ずダブらない1回目を無視すると、2回目でダブらない確率は 2/3。3回目でダブらない確率は 1/3。4回引く(必ずダブらない1回目を無視するので実質3回)場合の確率は
(2/3)*(1/3) + (1/3)*(2/3)*(1/3) + (2/3)*(2/3)*(1/3) = 0.44444…
3種類あるコンプガチャを4回で引く確率は 44.4%。期待値から計算した確率は55.2%(計算式は 1 - (1-(1/5.5))^4)
5回引く場合
(2/3)*(1/3) + (1/3)*(2/3)*(1/3) + (2/3)*(2/3)*(1/3) + ((1/3)^2)*(2/3)*(1/3) + (2/3)*(1/3)*(2/3)*(1/3) + (2/3)*((2/3)^2)*(1/3) = 0.6172
3種類あるコンプガチャを5回で引く確率は 61.7%。期待値から計算した確率は63.3%(計算式は 1 - (1-(1/5.5))^5)
外部リンク
アイテムコンプに必要なガチャの回数の期待値を厳密に計算する方法