How to calculate chance
The calculator is here.
The chance to get one or more when loot box of 1% chance is performed 100 times
This is same as the complementary event of the probability of losing all(100 times) when loot box of losing probability 99%. The calculation formula is as follows.
1 - 0.99100 = 63.4%
To calculate power on google, use ^. Googling following equation calculates above.
1 - 0.99^100
The chance to get two or more when playing loot box of 2% chance is performed 100 times
This is same as the complementary event of the probability of losing all and getting only once. To calculate the probability of getting specific number of times, use binomial distribution.
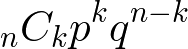
k:Number of winning
p:Probability of winning (chance)
q:Probability of Losing = 1-p
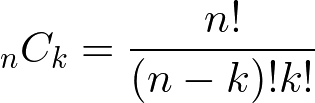
! is fractional. n! equals n(n-1)(n-2)……3*2*1。
The probability of losing all is 0.98100, the probability of getting only once is 100C10.0210.9899 . The calculation formula is as follows.
1 -0.98100 -100C10.0210.9899 = 1 -0.98100 -2*(0.9899) = 0.597 = 59.7%
To calculate combination (nCk) on WolframAlpha, enter C(n,k) in the search box.

To get with 99% chance, how many trials required when playing loot box of 2% chance
This is same as, to make the probability of losing under 1%, how many trials required when the probability of losing is 98%. The calculation formula is as follows.
0.98n < 0.01
= log 0.98n < log 0.01
= n * log 0.98 < log 0.01

Due to log 0.98 < 0, inequality sign is reversed.
Finally, n almost equals 228 .
Google can calculate log. To calculate above formula, enter log0.01/log0.98 in the search box.
The probability of kompu gacha
Coupon collector's problem (Wikipedia)
The expected value of loot box
When the chance is 1%, the expected value n is calculated with 1 = n * 0.01. In this cale, n is 100 (But the PROBABILITY is 63.4%).
2 varieties case
Since the first one does not duplicate, the expected value is 1. Due to The probability of duplicate is 1/2, the second chance is 1/2. Thus the expected value is 2. The sum of each (1 + 2 = 3) is the expected value of the kompu gacha.
3 varieties case
Since the first one does not duplicate, the expected value is 1. Due to the probability of duplication is 1/3, the secound chance is 2/3. Thus the expected value is 3/2. Because of the probability of duplication is 2/3, the third chance is 1/3. Thus the expected value is 3. The sum of each (1 + 3/2 + 3 = 5.5) is the expected value of the kompu gacha.