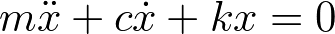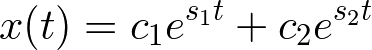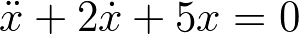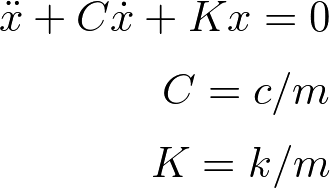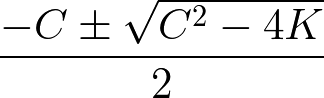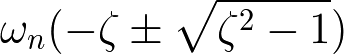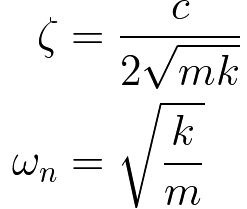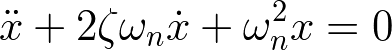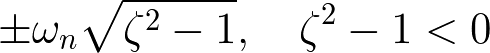固有振動数と減衰比の計算

カテゴリ：car

固有値（固有振動数ではない）の求め方

常微分方程式の固有値を無次元化して整理すると固有振動数と減衰比とが出てくる．まずは固有値を計算する．

運動を常微分方程式で表現すると以下のようになる．時間微分をドット・で表現する．

運動方程式

これは２階の線形常微分方程式なので一般解は以下のようになる．

上式の一般解

この s₁，s₂ を固有値（特性値・特性根）と呼ぶ．

例

固有値を求めるには方程式に一般解を代入し s₁，s₂ を計算する．例えば以下の方程式の固有値を求めてみる．

方程式例

(e^st)' = se^st，(e^st)'' = s²e^stより

(s² + 2s + 5)e^st = 0

e^st≠0 より

s² + 2s + 5 = 0

解の公式を使って解くと，固有値 s は -1 ± 2i になる．

振動数と減衰特性

固有値の実部の絶対値は減衰特性で，虚部の絶対値は振動数だ．上記の例では振動数は２，減衰特性は１になる．

固有値の実部の符号と虚部の符号とによって系が振動するか発散するかがきまる．まとめると以下のようになる．

	虚部 = 0（非振動）	虚部 ≠ 0（振動）
実部 = 0	一定値	一定振れ幅で振動
実部 < 0	非振動・減衰	振動・減衰
実部 > 0	非振動・発散	振動・発散

物理的な機械ではたいてい実部 < 0 で虚部≠0 になる．

無次元化

一般的な運動方程式は m，c，k の３つのパラメータがある．しかしこれを m で割ればパラメータを２つにできる．このように算術的にパラメータの数を減らす操作を無次元化と呼ぶ．

運動方程式

無次元化された方程式

すると固有値は以下のようになる．

無次元化された方程式の固有値

固有値の表現の変換

固有値の√の中身で系の振動の有無がきまる．この式を変形して振動と減衰とを把握しやすくする．

C = 2ζω_n ，K = ω_n² と置き換えると固有値は以下のように表現できる．ζはゼタ（ジータ）と読む．

無次元化された固有値

このζを減衰比とよび，ω_nを固有振動数とよぶ．それぞれ以下の式で計算できる．

減衰比ζと固有振動数ω_n

一般的にこの ω_n を固有振動数と呼んでいるが，これは固有角振動数[rad/s]だ．

この固有角振動数ω_n[rad/s]に 1/2π をかけると固有振動数[Hz]に変換できる．

元々の方程式は以下のようになる．

無次元化された方程式

固有振動数 ≠ 実際の振動数

振動数は固有値の虚部なので，無次元化された固有値の振動数は以下のようになる．

無次元化された固有値の振動数

√ζ²-1 の部分は減衰だ．減衰があればそれだけ振動数は少なくなる．ζ²-1 > 0 のとき，この系は振動しない．この状態を過減衰とよぶ．