DMD（Distribution Matching Distillation）のアルゴリズム

DMD1 が有名で DMD2 がその後継だが、DMD2 は GAN を使うため学習が不安定。なので DMD1 を使って蒸留モデルをつくることが多い。この記事では DMD1 の解説を行う。

学習データ

学習に使うのはノイズ画像とノイズ画像から生成された画像。

学習方法の概要

蒸留モデルの学習に KL 損失と LPIPS 損失を使う。

教師ノイズを蒸留モデルに入れて１ステップで画像を生成し、その画像と教師画像との損失を LPIPS で計算する。

蒸留モデルで生成した画像にノイズを付与し、ベースモデルと、fake data score function モデルとでデノイズし、正則化のための KL 損失を計算する。

よって３つのモデルが必要になる。

1. ベースモデル
2. 蒸留モデル。学習開始時にベースモデルで初期化される
3. fake data score function モデル。学習開始時にベースモデルで初期化される。このモデルは KL 損失を計算する際の損失を使って、蒸留モデルとは別に、同時に学習させる。

つまり通常の学習の約３倍の VRAM と計算時間とが必要になる。なお蒸留モデルと fake data score function モデルと二つのモデルを同時に学習させる。

アルゴリズム

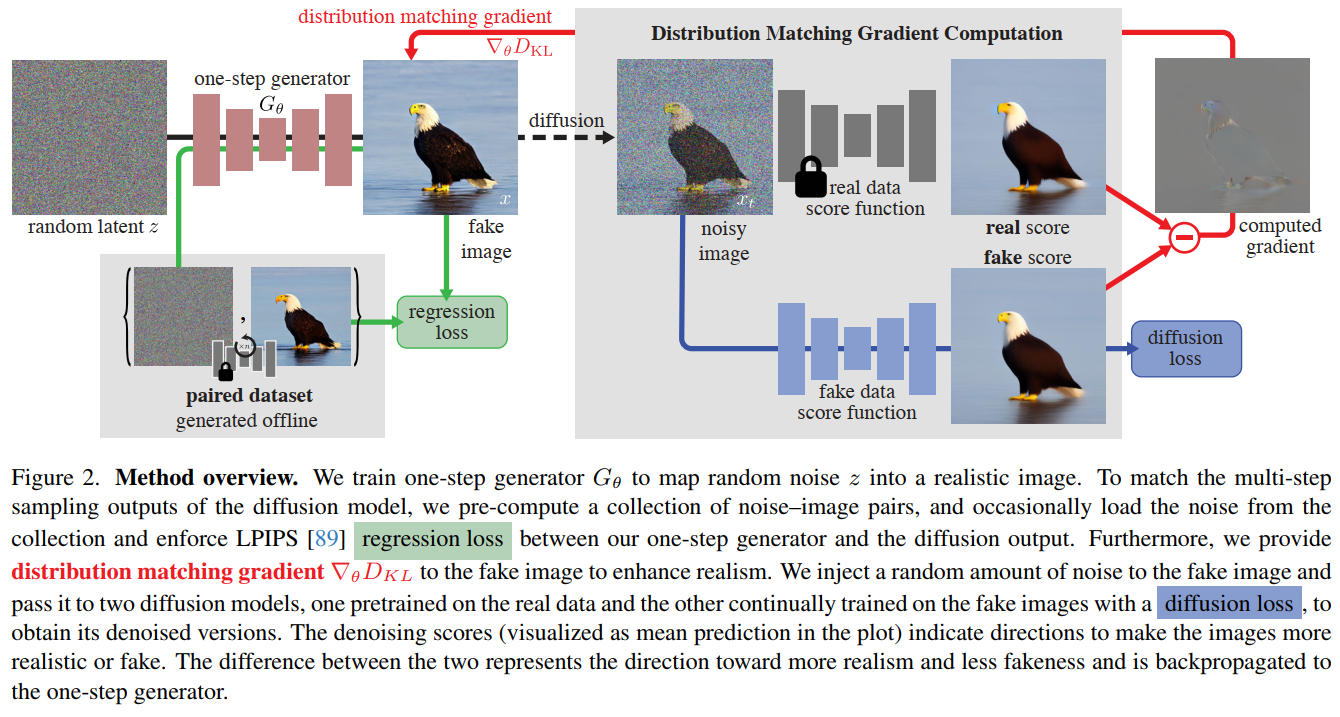
出典：One-step Diffusion with Distribution Matching Distillation Tianwei Yin et al. Figure. 2 https://arxiv.org/abs/2311.18828
蒸留モデル G は regression loss（LPIPS）と distribution matching gradient を使って学習させる。
fake data score function は G が生成した画像を使って普通に学習させる

記号

• $\mu_{base}$ 学習済みベースモデル（フリーズ）
• $G_\theta$ 訓練するモデル（蒸留モデル）
• $\mu_{base}(x_t, t)$ はノイズ予測（モデルはノイズを予測する $\epsilon \;\mathrm{pred}$ ）
• $\mu_{\mathrm{fake}}^\phi$ fake data score function モデル

$G_\theta$ と $\mu_{\mathrm{fake}}^\phi$ の初期ウェイトは $\mu_{base}$。

分布マッチング損失

real と fake との画像の分布 $p_{real}$ と $p_{fake}$ の KL を最小化する。

生成パラメータに対して勾配を計算すると：

s(x) はそれぞれの分布のスコア。

ノイズを付与したサンプル $x_t \sim q(x_t|x)$ は以下の式で定義：

スコアは以下の式で計算される：

蒸留モデルが更新されるので $\mu_{\mathrm{fake}}^\phi$ も更新する必要がある。$\mu_{\mathrm{fake}}^\phi$ の損失は以下の式になる：

通常の拡散モデルの学習と同様に、この損失はタイムステップ t に対応して適切にウェイトをかける必要がある。

分布マッチングの勾配更新

$w_t$ はタイムステップ依存のウェイトファクターで、ノイズレベルに応じて勾配の大きさを正規化する：

S は空間位置（spatial locations）の数で、C はチャンネル数。DreamFusion では $T_{min} = 0.02T, T_{max} = 0.98T$ を使用している。

回帰損失と最終的な損失関数

上記の分布マッチング損失は $t \gg 0$、つまりノイズが多い状況では機能する。しかしノイズ量が少ないと $p_{\mathrm{real}}(x_t, t)$ がゼロになるため、$s_{\mathrm{real}}(x_t, t)$ が不安定になる。

さらに、$\nabla_x \mathrm{log}(p)$ は確率密度関数 p のスケーリングに対し不変であり、最適化はモード崩壊（collapse）／モード脱落（dropping）の影響を受けやすく、fake の分布がモードのサブセットに全体的な密度を高く割り当てる現象が生じる。

これを回避するための回帰ロス（LPIPS）を追加した。

データセット $D = \{z, y\}$ の z はランダムガウスノイズ、y は $\mu_{\mathrm{base}}$ を使って z から生成した画像。

$\ell$ は LPIPS。$G_\theta(z)$ はタイムステップ入力がないのは 1 ステップで画像を生成するから。

最終的な損失関数は：

$\lambda_{\mathrm{reg}} = 0.25$ がデフォルト値。

CFG

CFG を使って学習するときは、キャプションを c、$\lambda_{CFG}$ を CFG スケールとすると $\nabla_\theta D_{\mathrm{KL}}$ は以下の式になる：

まとめ

1. KL の勾配は（理論的に）スコア $\nabla_\theta \mathrm{log} p$ の差で表せる

したがって分布整合（distribution matching）目的は「real のスコア − fake のスコア」を使った勾配で実行可能。

しかし実際の p の確率密度やスコアは高次元で直接計算できない。また、support が重ならないとスコアは発散したり（low-probability 領域で不安定）、fake サンプルに対して real スコアだけだと勾配が定義されない場合がある。

2. そこで「拡散（Gaussian ノイズ付与）して得られる“diffused”分布のスコア」を使う手法に落ち着く

Score-SDE の理論により、ノイズでぼかした分布ならスコアが安定して推定でき、その勾配は有効に定義される（分布の支持が重なるため）。なので論文は real と fake のそれぞれに対して 拡散済み分布のスコアを表現する 2 つのデノイザ（diffusion denoisers） を使って、KL の近似勾配を計算している。

なお fake 分布は蒸留中に変化するので、fake 側のスコアは学習（動的に更新）する必要がある。

3. 回帰損失（precomputed multi-step 出力との LPIPS 等の損失）を併用して正則化

score 差だけだとモード崩壊や多様性喪失が起こるので。

疑似コード

import torch
import torch.nn as nn
import torch.nn.functional as F
import lpips

# ---------------------------------------------------------
# LPIPS の初期化
# ---------------------------------------------------------
lpips_fn = lpips.LPIPS(net='vgg').to(device)
lpips_fn.eval()  # 推論モード

# ---------------------------------------------------------
# 事前に定義されていると仮定する関数・モデル
# ---------------------------------------------------------

class DiffusionModel(nn.Module):
    def forward(self, x, t):
        # スコア（ノイズ推定）を返す
        pass

class Generator(nn.Module):
    def forward(self, z):
        pass

def copy_weights(model):
    # モデルの重みコピー（疑似コード）
    new_model = type(model)()
    new_model.load_state_dict(model.state_dict().copy())
    return new_model

def distribution_matching_loss(mu_real, mu_fake, x):
    # KL 項に相当する損失 — Eq. 7
    pass

def forward_diffusion(x, t):
    # 前向き diffusion q(x_t | x_0) に相当
    pass

def denoising_loss(mu, x_t, x0_stop):
    # Denoising loss — Eq. 6
    pass

def lpips_loss(x1, x2):
    # LPIPS 損失 — Eq. 9
    return lpips_fn(x1, x2).mean()

# ---------------------------------------------------------
# DMD Training 本体
# ---------------------------------------------------------

def train_dmd(mu_real, dataset, num_steps=10000, lambda_reg=1.0, laion=False):

    # 1. Initialize generator + fake score estimator
    G = copy_weights(mu_real)
    mu_fake = copy_weights(mu_real)

    optimizer_G = torch.optim.Adam(G.parameters(), lr=1e-5)
    optimizer_fake = torch.optim.Adam(mu_fake.parameters(), lr=1e-5)

    step = 0
    while step < num_steps:
        step += 1

        # -------------------------------------------------
        # Generate images
        # -------------------------------------------------
        # 乱数 z, paired data (z_ref, y_ref)
        z = torch.randn(batch_size, latent_dim).to(device)
        z_ref, y_ref = next(dataset)  # (z_ref, y_ref) ~ D

        x = G(z)
        x_ref = G(z_ref)

        # LAION dataset なら concat(x, x_ref)
        x_input = torch.cat([x, x_ref], dim=1) if laion else x

        # -------------------------------------------------
        # Update generator: L_G = L_KL + λ * L_reg
        # -------------------------------------------------
        optimizer_G.zero_grad()

        L_KL = distribution_matching_loss(mu_real, mu_fake, x_input)  # Eq. 7
        L_reg = lpips_loss(x_ref, y_ref)                              # Eq. 9

        L_G = L_KL + lambda_reg * L_reg
        L_G.backward()
        optimizer_G.step()

        # -------------------------------------------------
        # Update fake score estimation model
        # -------------------------------------------------
        optimizer_fake.zero_grad()

        # time t ~ Uniform(0, 1)
        t = torch.rand(batch_size).to(device)

        # 前向き diffusion x_t = q(x_t | x)
        x_t = forward_diffusion(x.detach(), t)

        # Denoising loss: L_denoise
        L_denoise = denoising_loss(mu_fake, x_t, x.detach())  # Eq. 6

        L_denoise.backward()
        optimizer_fake.step()

        # -------------------------------------------------
        # ログ
        # -------------------------------------------------
        if step % 100 == 0:
            print(f"[{step}] L_G={L_G.item():.4f}, L_KL={L_KL.item():.4f}, L_reg={L_reg.item():.4f}, L_denoise={L_denoise.item():.4f}")

    return G

Decoupled DMD: CFG Augmentation as the Spear, Distribution Matching as the Shield

Decoupled DMD は CFG ありの DMD を分析し、CFG Augmentation 項と Distribution Matching 項とで違ったタイムステップスケジューラーを使うべき、と主張している。

CFG ありの DMD は以下のように変形できる。

DMD の $\mathrm{D_{KL}}$ 項は正則化だけではなく CFG Augmentation も行っていた。CFG Augmentation は低ステップ蒸留の本体で、Distribution Matching は学習を安定化させる正則化項。CFG Augmentation だけだと最初は画質が向上するが次第に崩壊する。Distribution Matching だけだと最初から崩壊する。

つまり DMD の画質向上の本質は CFG の焼きこみであって、分布マッチングではない。

正則化

Distribution Matching 以外の正則化として平均と分散を使う方法や GAN を使う方法がある。ここで品質と学習安定性のトレードオフがある。平均と分散を使う方法は安定しているが画質はそれほど向上しない。GAN は学習が不安定だが最高の品質を達成できる。Distribution Matching はその中間。

CFG Augmentation

CFG のタイムステップを制限したとき、[0.0, 0.05] つまり多いノイズで学習させたときは、構図や全体の色ブロックが強化された。逆に [0.7, 1.0] のような少ないノイズのみで学習させると、モデルが崩壊する。

これらの観察から、回帰損失の計算に使うタイムステップ t < CFG のタイムステップ τ に制限をかけた方がいい。

Distribution Matching

タイムステップ t が小さい（多ノイズ）の場合は全体の色や構図を修正し、t が大きい（小ノイズ）の時はテクスチャのアーティファクトを修正する。なので CFG Augmentation とは違いタイムステップに制限をかけない方がいい。

Distribution Matching Distillation Meets Reinforcement Learning

DMD に RL の損失を追加することで、品質を上げかつ報酬ハッキングも防ぐことができる。

DMD における Zero forcing 問題

DMD は生徒モデルが、教師 モデルのある生成モード (modes) を “カバーしきれず消失させてしまう (omit / drop)” zero forcing という現象がある。要は学習が不十分で、サンプルされる確率が低い分布を生徒が学習できないという現象。

単に DMD 損失 (distribution-matching) のみで蒸留を行うと、学習が学生モデルの「主な / 高頻度モード」に収束しやすく、低頻度モードのカバーは犠牲になる。

強化学習の追加

DMDR では、教師分布中の “重要だが低頻度” のモードも、たとえ頻度が低くても強化学習損失が「高報酬 (＝望ましい画像クオリティやプロンプト一致性など) 領域」と認めれば、学生モデルがそこを積極的に学ぶようになる可能性が高まる。これが、zero forcing のリスクを減らす。

DMD は分布マッチングの正則化が強力なので、強化学習の報酬ハッキングも防いでくれる。

報酬スコア

ReFL・DPO・GRPO を使うこともできる。

方法

任意の強化学習の損失を追加するだけ。

Dynamic Cold Start Stage

学習の初期段階では報酬モデルの報酬はノイジーで信用できないので、コールドスタート期間を設定した。

学習の初期段階では、多ステップで生成するモデルを１ステップで生成させているので全体的にボケた画像しか出力できない。これに対処する必要がある。

Dynamic Distribution Guidance (DynaDG)

学習の初期段階では real score estimator と fake score estimator との分布が違いすぎて、KL 正則化が不正確になる。

DMD では fake score estimator を通常の拡散モデル同様に学習させる。DMDR では fake score estimator をフリーズして LoRA に学習させる。学習させた LoRA をスケールを調整して fake score estimator だけでなく real score estimator にも適用する。

学習が進むにつれて LoRA スケールを弱くして本来の real score estimator の正則化が適用されるようにする。

Dynamic Renoise Sampling (DynaRS)

学習の初期段階では蒸留モデルにノイズの多い画像を学習させる。学習が進むにつれて一様分布のタイムステップでノイズを付与する。なぜなら、学習の初期段階でノイズの少ない部分（細部のディティール）を学習しても、ノイズの多い部分（構図や色）が間違っていたら意味がないから。