Wan2.2 の timestep 境界 0.875 の計算
0.875 にはならないが以下の方法で計算していると考えられる。
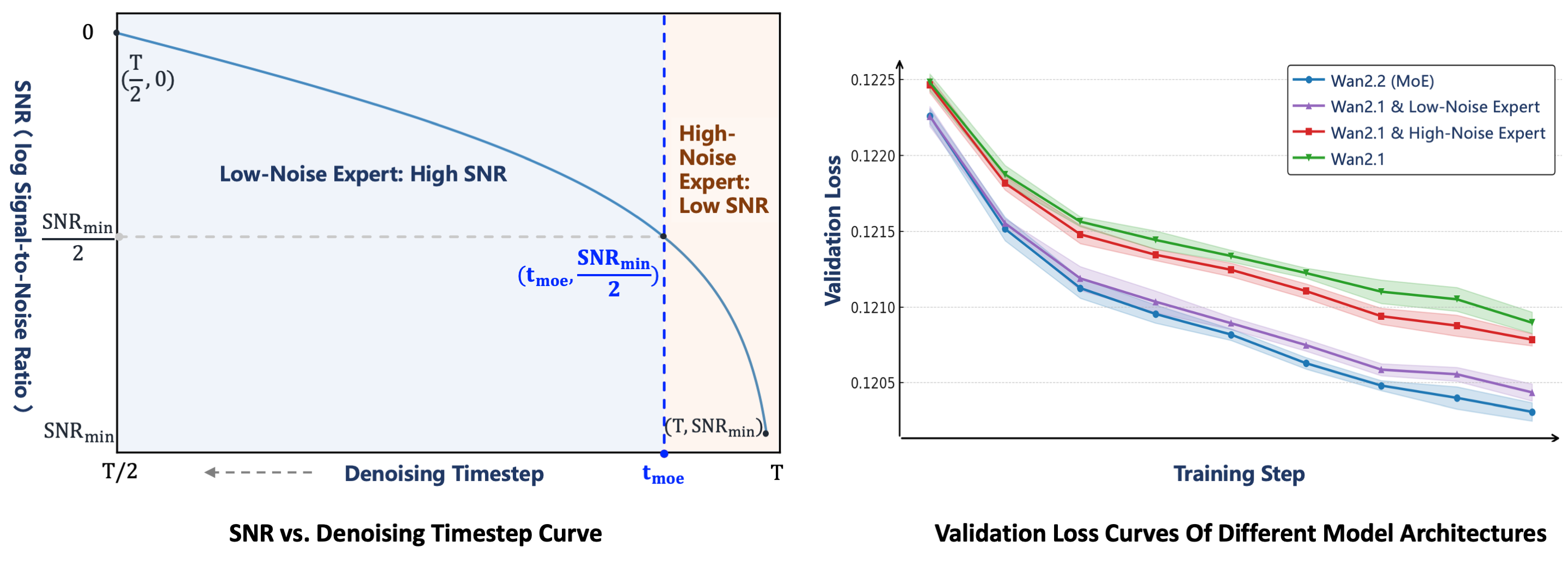
以下の図によると LogSNRmin/2 の場所で high と low のモデルを切り替えている。
出典：https://github.com/Wan-Video/Wan2.2/tree/main
SNR の計算
Rectifed Flow は タイムステップ t で画像とノイズとをブレンドするので、以下の式で SNR を計算できる。
\[ \mathrm{SNR} = \dfrac{(1-t)^2}{t^2}\]対数 SNR は以下のようになる。
\[ \mathrm{logSNR} = 2\mathrm{log}\dfrac{1-t}{t}\]lnSNRmin/2 の計算
t = 1 は計算できないので、t = 0.999 を使うと
\[ \begin{split} \mathrm{logSNR_{min}} &= 2\mathrm{log}(\dfrac{0.001}{0.999}) \\ \mathrm{\dfrac{logSNR_{min}}{2}} &\approx -3 \end{split}\]lnSNRmin/2 のときのタイムステップの計算
\[ \begin{split} -3 &= 2\mathrm{log}\dfrac{1-t}{t} \\ -1.5 &= \mathrm{log}\dfrac{1-t}{t} \\ 10^{-1.5} &= \dfrac{1-t}{t} \\ t &= \dfrac{1}{1+10^{-1.5}} \\ t &\approx 0.9693 \end{split}\]検算
\[ \mathrm{\dfrac{logSNR_{min}}{2}} \approx 2\mathrm{log}(\dfrac{1-0.9693}{0.9693}) \approx -3\]学習のノイズスケジューラーを調べて SNR の計算を修正すれば、0.875 になる可能性がある。
shift 込みの切り替えタイミング
タイムステップの shift は以下の式で計算される。s は shift 量。
\[ t^\prime = \dfrac{s\cdot t}{1 + (s-1)\cdot t}\]wan2.2 の T2V の切り替えタイミングは 0.850 が公式の値だ。切り替えタイミングの数式は以下のようになる。step - t になるのは、デノイズは逆拡散過程だから。t は切り替えステップ数で、step はデノイズステップ数。
\[ \dfrac{\mathrm{step} - t}{\mathrm{step}} \lt 0.850\](step - t)/step をそのまま shift で変換する（か 0.850 をタイムステップ変換の数式で逆変換する）と以下の式になる。
\[ t \gt \mathrm{step} - \dfrac{0.850\cdot \mathrm{step}}{s-(s-1)\cdot 0.850}\]ComfyUI の公式ワークフローでは t2v と i2v は s = 8、ti2v は s = 5。
s = 8、step = 20 のときは t > 11.71 なので、12 ステップで切り替えればよいということになる。
s = 5、step = 20 のとき t > 9.375。よって 10 ステップ。
外部リンク
Wan2.2のtimestep境界0.875はどこから来たのか？
Wan 2.2 misconception: the best high/low split is unknown and only partially knowable