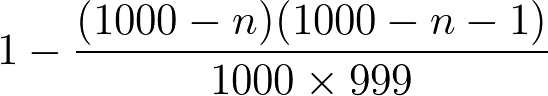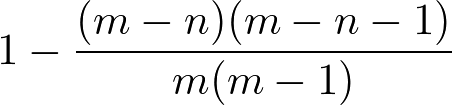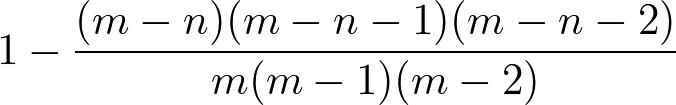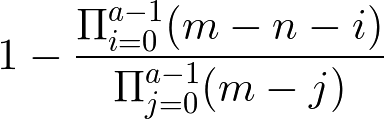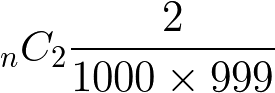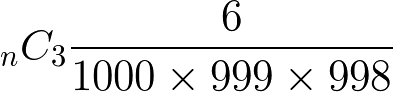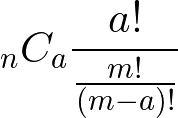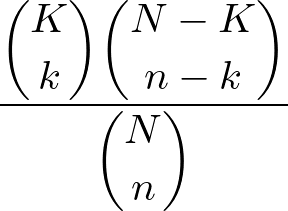ボックスガチャの確率計算

カテゴリ：statistics

この記事のボックスガチャは景品を引いても補充されず、各景品を引く確率は同様に確からしいとする。

１つしかないあたりを引く確率

ボックス内に景品が 1000 個入っていて、そのうちあたりが１個入っているとする。このときあたりを１回で引く確率は 1/1000 だ。

２回で引く確率は、１回で引く確率＋１回目を外して２回目で引く確率なので 1/1000 + (999/1000) * 1/999；つまり 2/1000。

３回で引く確率は、1/1000 + (999/1000) * 1/999 + (999/1000) * (998/999) * 1/998；つまり 3/1000。

まとめるとボックス内に景品が n 個入っていてあたりの個数が１個の場合、m 回ひいたときにそれが出る確率は m/n。

あたりをひとつも引かない確率の余事象を計算する。

まずあたりが２個の場合を考える。ボックス内に景品が 1000 個入っていて、そのうちあたりが２個入っている。

１回で引かない確率は 998/1000。

２回で引かない確率は (998/1000) * (997/999)；つまり(998*997)/(1000*999)

３回で引かない確率は (998/1000)*(997/999)*(996/998)；約分すると (997*996)/(1000*999)。

４回で引かない確率は (998/1000) * (997/999) * (996/998) * 995/997；約分すると (996*995)/(1000*999) 。

これを n 回引いたとき（有効な n は 1 <= n <= 999）あたりをひとつも引かない確率は、

((1000-n)*(1000-n-1))/(1000*999)

引く回数を n とすると、あたりをひとつも引かない確率の余事象なので以下のようになる。

ボックス内に景品が m 個入っていて、そのうちあたりが２個入っている。そして景品を引いてもボックスが補充されないとする。このときボックス内から n 個引いた時ひとつ以上当たる確率は以下のようになる。

ボックス内に景品が m 個入っていて、そのうちあたりが２個入っている場合の計算式

ボックス内に景品が m 個入っていて、n 回引く。３個あるあたりのどれかひとつ以上を引く確率の計算式

ボックス内に景品が m 個入っていて、そのうちあたりが a 個入っている。景品を引く確率はすべて等しく、景品を引いてもボックスが補充されないとする。このときボックス内から n 個引いた時ひとつ以上当たる確率は以下のようになる。

ボックス内に景品が m 個入っていて、そのうちあたりが a 個入っている場合の計算式

ボックス内に景品が 1000 個入っていて、そのうちあたりが２個入っている。

このボックスから３回引いたとき、あたりふたつを引く場合の組み合わせは以下のようになる。

確率はそれぞれ(2/1000)*(1/999)*(998/998)、(2/1000)*(998/999)*(1/997)、(998/1000)*(2/999)*(1/998)。まとめると (3*2)/(1000*999)。

４回の場合も同様に計算すると(6*2)/(1000*999)になる。

景品数が 1000 で、あたりの数が２、引く回数を n とするとあたりをすべて引く確率は以下のようになる。

景品数が 1000 であたりの数が３、引く回数を n とするとあたりをすべて引く確率は以下のようになる。

ボックス内に景品が m 個入っていて、そのうちあたりが a 個入っている。そして景品を引いてもボックスが補充されないとする。これを n 回引いた時あたりをすべて引く確率は以下のようになる。