G*Power 3.1.9.2 を使ってサンプルサイズを計算する(t 検定・対応のないデータ)
この記事では対応のないデータの平均を t 検定で検定する際のサンプルサイズを G*Power で計算する方法を解説する。
入手方法
G*Power は HEINRICH HEINE からダウンロードできる。
G*Power のマニュアル
解説記事
効果量と検定力分析入門―統計的検定を正しく使うために―(pdf)
A Power Primer(Jacob Cohen, 1992)(pdf)
対応とは
データを取る対象が同じ場合、対応のあるデータとなる。例えば以下のようなデータだ。
- 同じ被験者の、ダイエット食品の試用前と後との体重
- ある店舗の販促前と後との売上
対応のないデータとは、例えば肥料Aと肥料Bとで育てた野菜の質量のようなデータのこと。
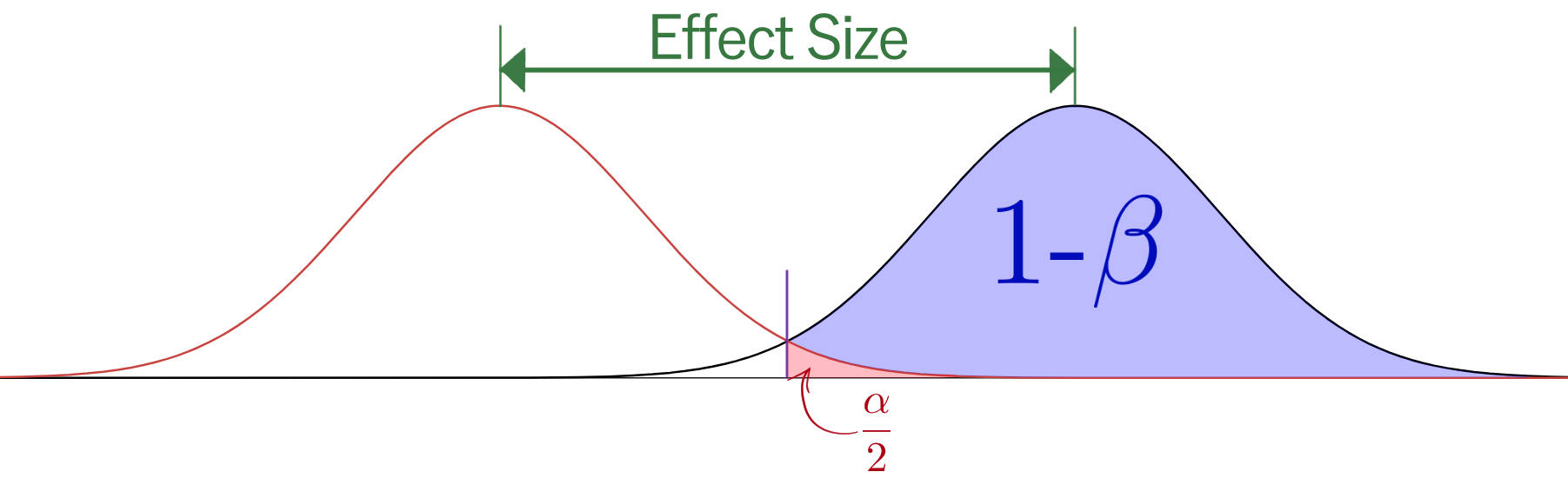
なぜサンプルサイズの計算に Effect Size が必要なのか
Effect Size を雑に説明すると、検定しようとするパラメータの差の大きさだ。たとえば地域ごとの平均身長の差を検定するとする。この時、小数のサンプルから計算した地区Aの平均身長が平均 170 cm、地区 B は 150cm だった場合、Effect Size が大きい(平均の差が大きい)ので小数のサンプルで有意差がでる。逆に地区Aと平均身長が 170.5cm の地区Cとを検定する場合、多数のサンプルが必要になる。
データを集める前に Effect Size を知ることは不可能だが、小数のサンプルから Effect Size を概算することは可能だ。
α・1-β・Effect Size
サンプルサイズ N は α・1-β・Effect Size を決めることで計算できる。
使い方
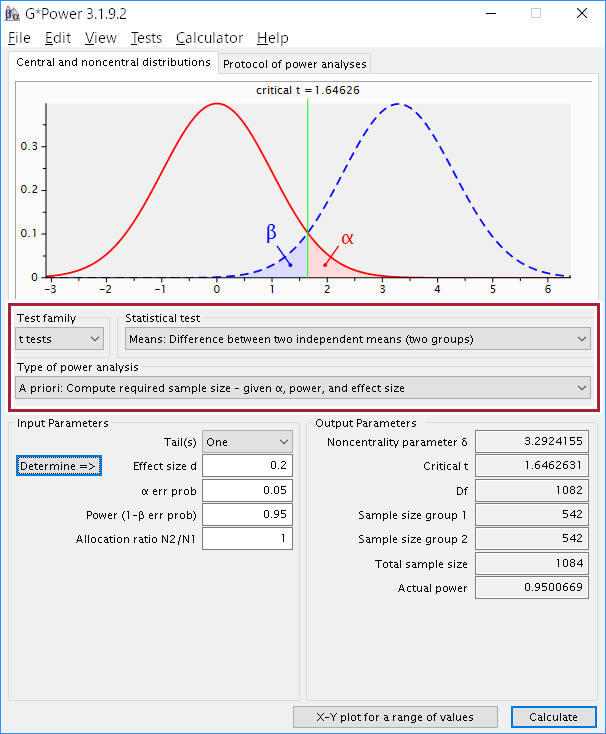
対応のないデータの t 検定のサンプルサイズをきめる場合、上3つのドロップダウンボックスを以下のように設定する。
Input Parameters の設定
Tail(s)
両側検定の時は Two、片側検定の時は One を指定する。
Effect Size d
効果量の大きさで小の時は 0.2、中の時は 0.5、大の時は 0.8 を指定する。この検定の場合効果量の大きさは、平均値の差の大きさを指定することになる。効果量が1の時、ちょうど分散の量だけ平均値との差があることになる。
α err prob
有意水準で 0.05(5%)や 0.01(1%)を指定することが多い。
Power(1-β err prob)
検定力で 0.8 がよく使われる。これは「本当は差があるのに差がない」と判定する確率で、0.8 の場合 20% の確率で「本当は差があるのに差がない」と判定してしまう。
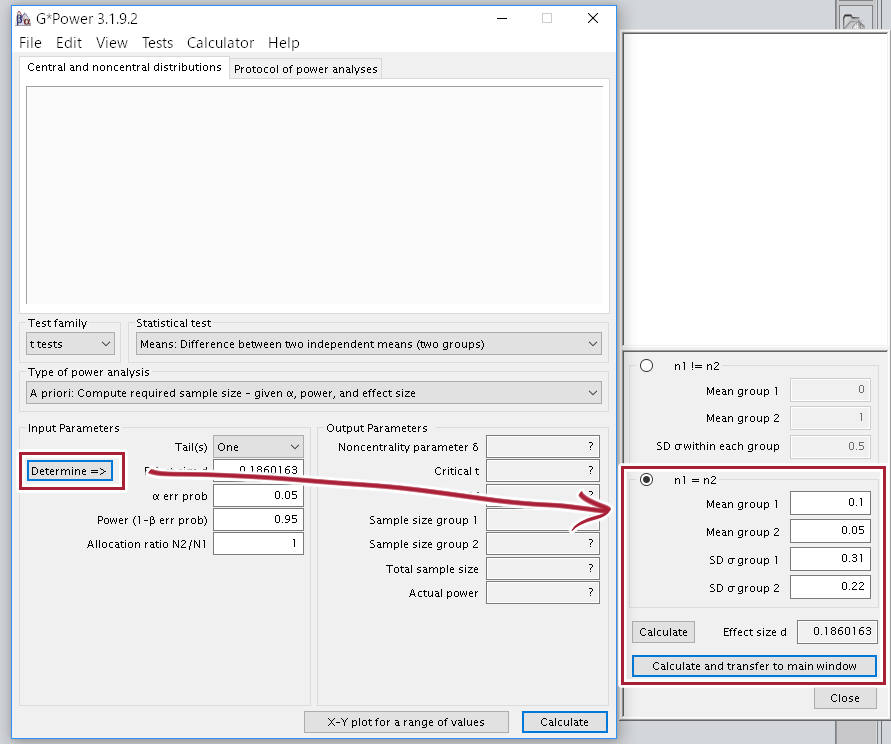
Effect Size d の計算
Determin => をクリックすると効果量を計算するウインドウが現れる。ここに平均値と分散を入力し、Calculate を押すと計算される。Calculate and transfer to main window を押すとメインウインドウに反映される。
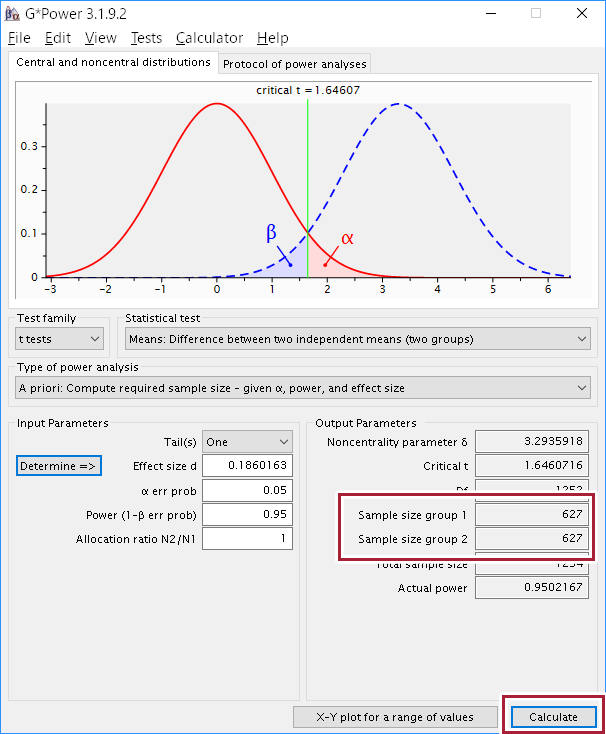
計算
後はメインウインドウで Calculate を押せば Sample size group 1,2 のところにサンプルサイズが表示される。