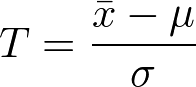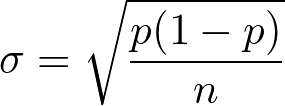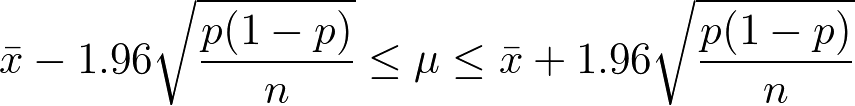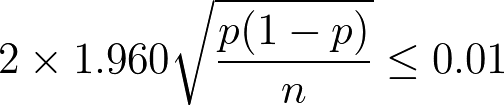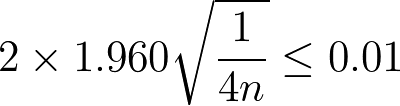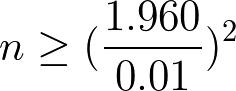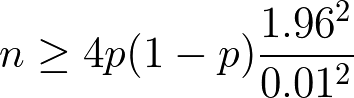ドロップ率の検定
大標本（np > 5）の場合
ドロップ率５％の場所で、200 回戦闘して宝箱が 19 個ドロップした（標準偏差 0.021）。このとき宝箱のドロップ率は５％より多いと言えるか＜有意水準１％＞。
検定統計量 T は以下のようになる。
大標本の z 検定
μ ：A の標本比率（この場合は 0.05）
σ1：B の標準偏差（この場合は 0.021）
大標本（np > 5）なので二項分布を正規分布で近似できる。この時の標準偏差は以下のようになる。
二項分布を正規分布で近似したときの標準偏差の計算式
p：ドロップ率（この場合は 0.095）
n：試行回数（この場合は 200）
大きいことを検定したいので右片側検定を行う。有意水準１％なので検定統計量 T が 2.33 より大きい時、差があるといえる。
この例では検定統計量 T = 2.17。T < 2.33 なので差があるとはいえない。
有意水準５％で検定する場合は 1.65 と比較する。その場合はこの例では差があることになる。そのほかの有意水準の場合はt 分布パーセント点分布表を参照。自由度 200 の部分を参照する。
p 値
検定統計量 T がわかれば下のリンク先の表から p 値を計算できる。T = 2.17 に対応する p 値は 0.015 だ。
95％信頼区間
正規分布で近似した二項分布の 95％信頼区間は以下の式で計算できる。
95％信頼区間の計算式
この例の 95％信頼区間は 0.0544～0.1356。
99％信頼区間を計算するときは 1.96 の代わりに 2.58 を使う。
信頼区間の解釈についての注意
信頼区間は真のドロップ率を与えるものではない。さらに 95 ％信頼区間は 95 ％の確率で真の値がその区間にあるわけではない。95 ％信頼区間は「同じ実験を繰り返し実行し複数個の信頼区間を得たとき、95 ％の確率でそれらの信頼区間の中に真の値が含まれる」という意味だ。
例えば、学校が 100 校あり、それぞれの学校で平均身長を計算するとする。あるひとつの学校が自校の平均身長の 95%信頼区間を計算した場合、他の 95 校の平均身長がその信頼区間の範囲内に収まる。
詳細は「信頼区間」が意味するものを参照。
上記のガチャの信頼区間の解釈は『この試験を 100 回繰り返したとき、そのうちの 95 個のドロップ率は 5.44 ％～ 13.56％の間におさまる』になる。
真のドロップ率を検証する方法はない。
小標本の場合
ドロップ率５％の場所で、31 回戦闘して宝箱が７個ドロップした（標準偏差 0.075）。このとき宝箱のドロップ率は５％より多いと言えるか＜有意水準１％＞。
検定統計量 T は大標本の時と同じ。ただし参照する値はt分布表になる。自由度 degrees of freedom はサンプル数－１であることに注意。
大きいことを検定したいので右片側検定を行う。自由度 30(31-1)・片側有意水準１％なので検定統計量 T が 2.46 より大きい時、差があるといえる。
この例では検定統計量 T = 2.34。T < 2.46 なので差があるとはいえない。
サンプルサイズの計算
欲しい信頼区間を決めれば必要なサンプルサイズを計算できる。例えば95%信頼区間で欲しい区間を1%（つまり ±0.5%）に設定するならば以下の式を解けばいい。
p が不明の場合はここで p = 0.5 を使う。なぜならその値で p(1-p) が最大値になるからだ。前もっておおまかに p がわかっているなら、0.5 でなくその値を 0.5 に近づくように切り上げ/切り下げた値を使う。p = 0.5 を使った場合、上記の式は以下の式になる。
これを n について解くと以下の式になる。
この場合 n は 38,416 になる。
以下のようにして書くと計算しやすい。99％信頼区間を計算するときは 1.96 の代わりに 2.58 を使う。
