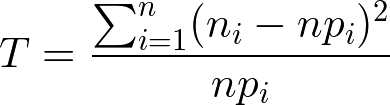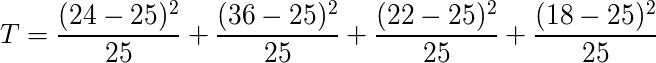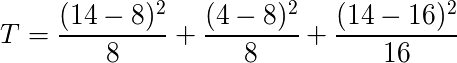ドロップの偏りの検定
カテゴリ：statistics
等確率の場合
宝箱から４種類アイテムが等確率（つまり25％）でドロップするとされる場所で、以下のようなドロップ結果になった。この場所のアイテムドロップ率は等確率か？＜有意水準５％＞
| アイテムＡ | 24 |
| アイテムＢ | 36 |
| アイテムＣ | 22 |
| アイテムＤ | 18 |
検定統計量の計算
χ2（カイじじょう）検定を行う。検定統計量Ｔは以下のようになる。
χ2検定の検定統計量Ｔ
n：種類の数（この例では４）
ni：実測度数（この例ではそれぞれのドロップ数）
npi：期待度数（この例では 100*0.25 = 25）
展開して書くと以下のようになる。
実際の計算式
検定統計量Ｔは 7.2。比較する値はχ2分布表から 7.81。
この例では T > 7.81 のとき差があるといえる。
T < 7.81 なので差があるとは言えない。
つまり等確率かもしれないし、そうでないかもしれない。
χ2分布表の読み方
この例では有意水準５％なので 0.05、自由度は種類の数－１なので３の場所を参照する。
確率が異なる場合
宝箱から３種類のアイテムがドロップする場所し、アイテムＡ・Ｂはそれぞれ 25 ％、アイテムＣは 50 ％の確率でドロップするとされている場所で以下のようなドロップ結果になった。この場所のアイテムドロップ率は公表と差があるといえるか？＜有意水準５％＞
| アイテムＡ | 14 |
| アイテムＢ | 4 |
| アイテムＣ | 14 |
検定統計量の計算方法は同じだ。展開して書くと以下のようになる。
検定統計量Ｔは 6.75。自由度は２で有意水準は５％なので、比較する値は 5.99。T > 5.99 なので差があるといえる。